Difference hierarchy

In set theory, the difference hierarchy over a pointclass is a hierarchy of larger pointclasses generated by taking differences of sets. If Γ is a pointclass, then the set of differences in Γ is 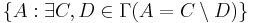$\{A:\exists C,D\in\Gamma ( A = C\setminus D)\}$ . In usual notation, this set is denoted by 2-Γ. The next level of the hierarchy is denoted by 3-Γ and consists of differences of three sets: 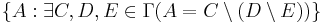$\{A�: \exists C,D,E\in\Gamma ( A=C\setminus(D\setminus E))\}$ . This definition can be extended recursively into the transfinite to α-Γ for some ordinal α.

In the Borel and projective hierarchies, Felix Hausdorff proved that the countable levels of the difference hierarchy over Π⁰_γ and Π¹_γ give Δ⁰_γ+1 and Δ¹_γ+1, respectively.